[게임 이론] 31 게임 이론
둘이서 진행하는 31 게임의 필승법을 알아봅니다.
31 게임 필승법
31 게임의 규칙은 나와 상대가 번갈아 가면서 숫자를 부르는데 한 번에 3개까지 가능하며 31을 부르는 사람이 집니다.
31 게임을 무조건 이기기 위해서는 한 가지 조건이 있는데 선공을 해야합니다.
그리고 처음에 번호를 부를 때 정해진 수까지를 불러야 하는데, 그 수는 2입니다.
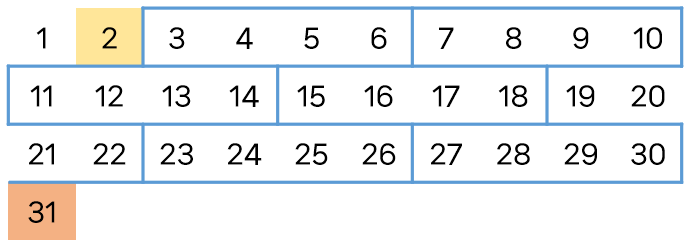
그래서 처음 턴에 2까지 부르고 상대에게 턴을 넘깁니다.
그 이후로는 (상대 -> 나) -> (상대 -> 나) -> … 순서로 진행되는데
이때 상대와 내가 부르는 수가 4개가 되게 불러야 합니다.
그렇게 불러 나가다 보면 무조건 상대가 31을 부르게 됩니다.
이해하기 쉽게 그림으로 보면 이렇게 표현할 수 있습니다.
31 게임 필승법의 일반식
위의 방법은 부르면 지는 수와 한 번에 부를 수 있는 수를 바꿔도 적용됩니다.
필승법을 일반식으로 나타내면:
부르면 지는 수를 j라고 하고 한 번에 부를 수 있는 수를 m이라고 했을 때,
처음에 번호를 말할 때 말해야 하는 마지막 수 r =
(j - 1) % (m + 1)(상대 -> 나) 턴에 말해야 하는 수의 길이 =
m + 1
입니다.
일반식의 적용과 원리
일반식을 다른 예제로 확인해보겠습니다.
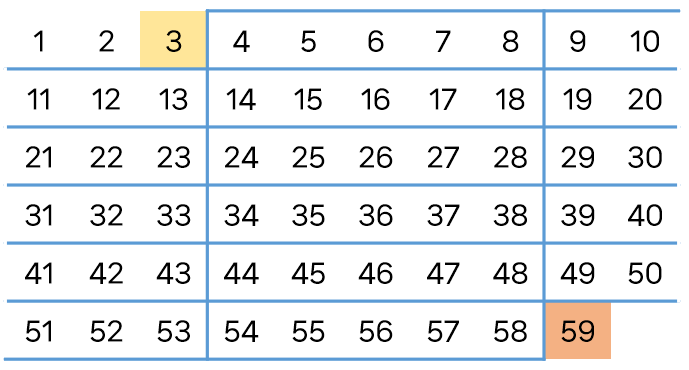
부르면 지는 수 j가 59이고 한 번에 부를 수 있는 수 m이 4인 경우를 확인해보겠습니다.
그럼 처음에 번호를 말할 때 말해야 하는 마지막 수 r = (j - 1) % (m + 1) = 3
(상대 -> 나) 턴에 말해야 하는 수의 길이 = m + 1 = 5 입니다.
이것도 그림으로 한 번 보겠습니다.
그림으로도 볼 수 있다시피 일반식이 이렇게 나오는 이유는 마지막 수부터 거꾸로 생각해보면 쉽게 생각할 수 있습니다.
상대방이 불러야 하는 마지막 수를 빼면 그 직전 차례는 본인의 차레이고,
상대방이 부르는 수에 맞춰서 본인의 수를 조절할 수 있게 (상대방 -> 본인)의 턴을 묶어서 생각하며,
한 묶음에서 불러야 하는 개수를 상대방이 1에서 m까지 어떤 수를 부르든 맞출 수 있는 m + 1개로 설정하고,
그렇게 묶어내고 나서 남은 처음 수들을 처음에 번호를 말할 때 말해야 하는 마지막 수로 정하여
공식으로 나타낸 것입니다.
✨ 핵심 포인트
둘이서 하는 31 게임 필승법:
- 선공으로 시작한다.
부르면 지는 수를 j라고 하고 한 번에 부를 수 있는 수를 m이라고 했을 때,
처음에
(j - 1) % (m + 1)까지 부른다.(상대 + 나)으로 두 차례를 하나로 묶어서 상대방이 부르는 개수와 내가 부르는 개수를 합쳐서
m + 1이 나오게 부른다.