[BOJ/백준] 11653번 : 소인수분해 (Java)

11653번 : 소인수분해 (https://www.acmicpc.net/problem/11653)

---

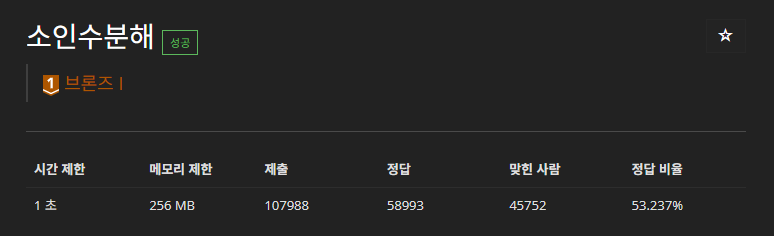
문제

---

접근 방법

---

첫 번째 접근 (풀이 1)

• N이 1이 될 때까지 어떤 수로 나누어 본다. 여기서 어떤 수는 2부터 1씩 증가시키며, 나누어 떨어지면 그 수는 소인수이다.

• 어떤 수로 나누었을 때 나누어 떨어지면 다음 반복에서 해당 수를 한 번 더 나누어서, 해당 수가 몇 번 곱해지는지 알아낸다.

• 이 방법은 나누는 수를 2부터 하나씩 증가시키고 최악의 경우 N이 될 때까지 반복할 수 있기 때문에 시간 복잡도는 O(N)이다.

• N의 범위가 1 ≤ N ≤ 10,000,000이므로 O(N)으로도 해결할 수 있지만, 더 빠른 방법이 존재한다.

  
  

두 번째 접근 (풀이 2)

• 첫 번째 접근에서 소인수를 찾았을 때 해당 소인수가 몇 번 곱해지는지 확인하기 위해 다음 반복에서 나누는 값을 그대로 유지한 채 반복하였는데, 두 번째 접근에서는 내부 반복문을 이용하여 확인하였다.

• for 반복문을 사용하여 나누는 값의 범위를 2부터 sqrt(N)까지로 지정하였다.

  √N까지만 확인해도 되는 이유

  N이 합성수일 때, N = a * b(a, b는 자연수)로 나타낼 수 있으며, 둘 중 하나는 반드시 √N 이하의 값이 된다. √N보다 큰 값은 그 값에 대하여 소인수분해를 할 수 있기 때문에 √N까지만 확인하여도 된다. N이 소수인 경우는 반복문 밑에서 처리한다.

• 반복문에서 N이 1이 되면 소인수분해가 끝난 것이기 때문에 반복문을 탈출한다.
• 만약 해당 수로 N이 나누어 떨어지면 해당 수를 소인수로 같은 것이므로 내부 while문을 사용하여 해당 수가 몇 번 곱해져 있는지 확인한다.
  • 확인하는 방법은 해당 수로 나누어 떨어지지 않을 때까지 나누면 된다.
• for 반복문이 끝났을 때 N이 1이 아니면 N은 소수인 것이므로 N을 출력한다.
  • 1이 아니면 저장된 출력문을 출력한다.

• 이 방법은 for 반복문에서 O(√N), 내부 while문에서 O(logN)이므로 전체 시간 복잡도는 O(√N × logN)이 된다.

• 첫 번째 방법의 시간 복잡도인 O(N)보다 두 번째 방법의 시간 복잡도인 O(√N * logN)이 더 빠르다.

코드

---

풀이 1 - N이 1이 될 때까지 나누는 수를 하나씩 증가시키고 나누어 떨어지면 해당 값을 한 번 더 반복

import java.io.*;

public class Main {
	public static void main(String[] args) throws IOException {
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
		StringBuilder sb = new StringBuilder();
		int N = Integer.parseInt(br.readLine());
		int i = 2;
		while (N > 1) {
			if (N % i == 0) {
				sb.append(i).append("\n");
				N /= i;
			} else {
				i++;
			}
		}
		bw.write(sb.toString());
		bw.flush();
		bw.close();
		br.close();
	}
}

*위의 코드의 성능_

풀이 2 - N이 1이 될 때까지 나누는 수를 2부터 sqrt(N)까지로 하나씩 확인하면서 소인수이면 몇 제곱인지 확인하기

import java.io.*;

public class Main {
	public static void main(String[] args) throws IOException {
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
		StringBuilder sb = new StringBuilder();
		int N = Integer.parseInt(br.readLine());
		int end = (int) Math.sqrt(N);
		for (int i = 2; i <= end; i++) {
			if (N == 1)
				break;
			while (N % i == 0) {
				sb.append(i).append("\n");
				N /= i;
			}
		}
		if (N != 1) {
			sb.append(N).append("\n");
		}
		bw.write(sb.toString());
		bw.flush();
		bw.close();
		br.close();
	}
}

위의 코드의 성능

정리

---

소수와 관련된 소인수분해, 약수와 관련된 알고리즘은 sqrt(N)을 항상 생각해야 한다.